INF1010 3WB – Lista 6: Grafos.

Exercícios

1. Dado o grafo não direcionado e ponderado ilustrado abaixo, responda as questões a seguir:
   
   
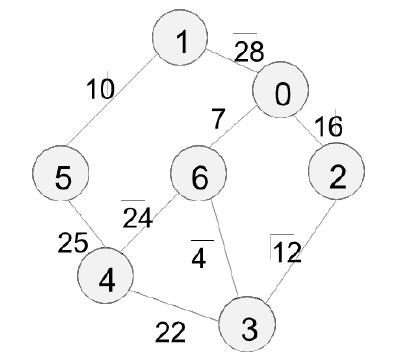
   1. Mostre como seria a sua representação por matriz de adjacências.
   2. Mostre como seria a sua representação por lista de adjacências.
   3. Em que ordem os vértices são visitados em uma execução de uma BFS a partir do vértice 0? E a partir do vértice 3? (Considere a ordem definida por você na sua representação por lista de adjacências).
   4. Em que ordem os vértices são visitados em uma execução de uma DFS a partir do vértice 5? E a partir do vértice 0? (Considere a ordem definida por você na sua representação por lista de adjacências).


2. A figura abaixo mostra um rato (🐀) que está em busca de um caminho num labirinto que o leve até um queijo (🧀). O rato caminha pelo labirinto sabendo por onde ele já passou (acho que ele vai marcando com pedrinhas). Quando ele começa a andar ele segue em frente até que encontre uma parede ou um entroncamento (lugar onde ele pode ir para mais de uma direção). Quando não existe outra opção, ele volta até achar um entroncamento onde exista outra rota não explorada e segue por ela. Ele é muito sistemático, sempre tenta primeiro ir para o Sul (abaixo). Se não puder vai para o Leste (direita). Não podendo nenhuma das duas direções, tenta o Norte (acima) e por último o Oeste (esquerda).
   
   
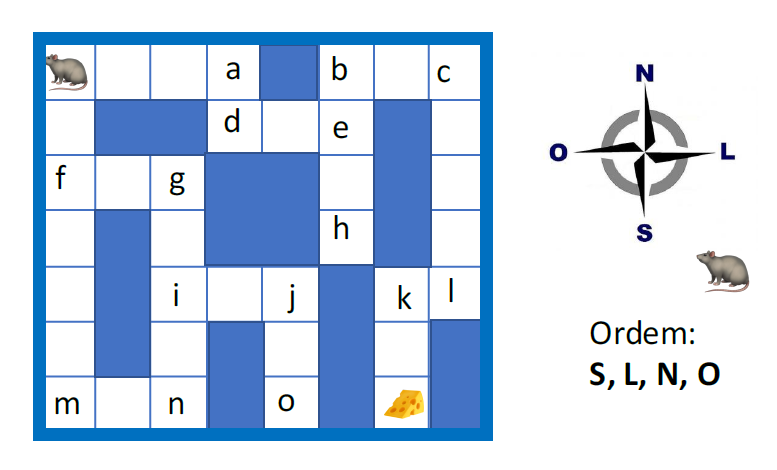
   1. Descreva o problema em termos de um grafo. Mostre todos os passos do caminho que o rato faz até chegar no queijo. Use a notação (x→y→z).
   2. Que algoritmo de grafo é este? Explique através de um pseudocódigo como este algoritmo funciona. Este pseudocódigo trata de grafos desconexos? Se não, mostre como ele pode ser estendido. (obs. O seu pseudocódigo não precisa incluir variáveis ou detalhes que não são relevantes para o problema do rato, a menos da questão de grafos desconexos).


3. Para o mesmo grafo da primeira questão, determine a distância mínima de todos os vértices ao vértice 0, de acordo com o algoritmo de Dijkstra. Mostre passo-a-passo como o algoritmo funciona.


4. Para o mesmo grafo da primeira questão, mostre o passo a passo do algoritmo de Kruskal para cálculo da árvore geradora mínima. Em cada passo do algoritmo mostre como ficaria a partição dinâmica dos nós utilizando a notação de conjuntos (ex.:{ {a,c}, {b,e,f}, {d}} ).


5. Escreva um algoritmo que verifique se existe ciclo num grafo representado por lista de adjacências.