INF1010 3WB – Lista 3: Heap.

Exercícios

1. Enuncie a(s) característica(s) que define(m) um heap e diga se cada um dos grafos a seguir são ou não são um heap.
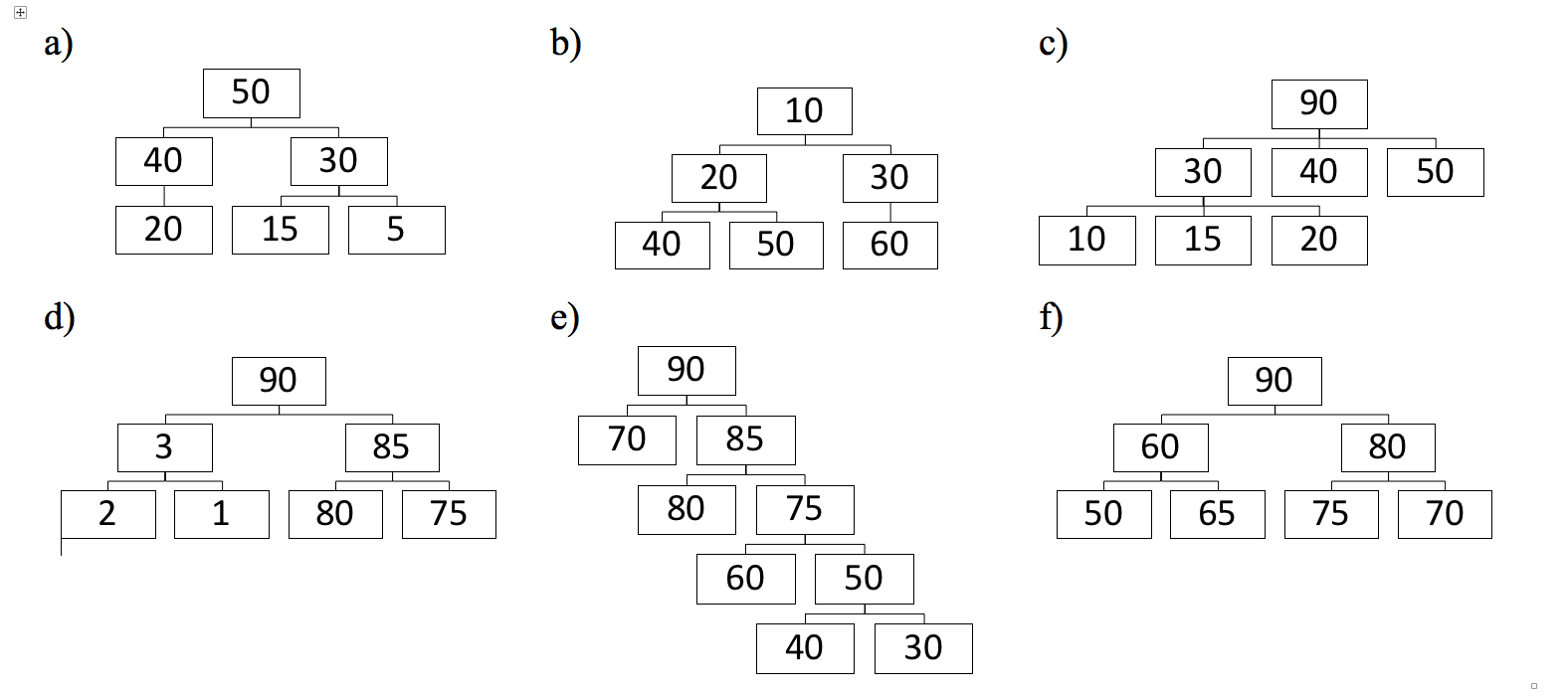
2. Explique com palavras o algoritmo de remoção da prioridade que está no topo de um heap de máximo. Mostre também a implementação da função heap_remove de acordo com a estrutura e o protótipo dados abaixo. Para simplificar assuma que o heap existe e que tem pelo menos um elemento. Ou seja, não trate destes casos. Se você utilizar alguma função auxiliar apresente a implementação dela também.
3. Considere o vetor de heap = (95,60,78,39,28,66,70,33). Mostre passo a passo quais seriam as modificações que o vetor sofre quando:
   1. é retirado o elemento do topo;
   2. é inserido o um elemento com a prioridade 50 (no vetor original).
   3. é aplicado o algoritmo de heapsort.
4. Considere o vetor de chaves de prioridade {30,15,28,60,45,90,10,23}.
   1. Construa um heap de máximo inserindo uma chave de cada vez seguindo a ordem do vetor.
   2. Construa um heap de máximo fazendo o menor número de trocas possível.
   3. Qual a complexidade de cada uma das operações acima?
   4. Os vetores/árvores dos heaps dos casos (a) e (b) são iguais?
5. Escreva uma função que verifica se um vetor armazena um heap de máximo. Utilize o seguinte protótipo.

bool verifica_heap(int n, float* prioridade);

6. implemente as cinco funções de uma classe de Heap de mínimo, cuja interface é:

   class Heap /* Min-Heap */
   {
   public:
       //Construtor vazio
       Heap();
   
       //Constroi o heap a partir de um vetor de prioridades
       Heap(int n, float* prioridade);
   
       //Destroi o heap
       ~Heap();
   
       //Insere um novo elemento
       void insere(float prioridade);
   
       //Remove o elemento do topo e retorna sua prioridade
       float remove();
   
   private:
       int _n;               // numero de elementos
       float* _prioridades;  //Contem os elementos do heap
   };
   
   

7. Considere o vetor de heap mostrado abaixo. Mostre quais seriam as modificações que o algoritmo de inserção do valor 50 provocaria no vetor. Ou seja, mostre explicando como o vetor iria se modificando, chegando até ao heap final.

   95,60,78,39,28,66,70,33