Trabalho de Geom.
Computacional (2003.1)
Reconstrução de curvas no
plano
Alunos:
Antonio Luiz Vitalo Calomeni
Manuel Eduardo Loaiza Fernández
Rodrigo de Souza Lima Espinha
Implementação (CGAL 2.4, Linux 2.4, gcc 2.95), utilizando OpenGL
1. Introdução
Em algumas aplicações é necessário reconhecer formas de objetos pelas suas fronteiras, e as informações que possuímos são amostras de pontos obtidos de uma imagem, por exemplo. Este é um problema comum em visão computacional.
Podemos, então, reconstruir a curva que define a fronteira de um objeto, mas isto depende sempre da determinação de uma condição ou critério para definir os pontos e arestas que fazem parte da curva ou não.
Vários algoritmos foram propostos para resolver esse problema. Aqui, apresentaremos três algoritmos: Crust e Beta-Skeleton, que possuem características semelhantes, e Gathan, que se propõe a reconstruir curvas com cantos vivos (“sharp corners”).
2. Reconstrução de curvas suaves
Dois grafos de proximidade que podem ser utilizados para reconstrução poligonal de curvas a partir de amostras suficientemente densas de pontos no plano são: Crust e Beta-Skeleton. Esta seção baseia-se no artigo: “The Crust and the Beta-Skeleton: Combinatorial Curve Reconstruction”, por N. Amenta, M. Bern e D. Eppstein [1], onde é demonstrado que, sob certas condições de amostragem, pode-se garantir que ambos os grafos reconstruam uma curva suave, contínua, fechada e sem auto-interseções, por sua aproximação poligonal mais provável. O objetivo final é obter uma aproximação poligonal que conecte exatamente todas as amostras adjacentes ao longo da curva.
A seguir, serão expostos alguns teoremas e definições relativos a Crust e Beta-Skeleton, extraídos de [1], e que não serão provados aqui. Além disso, serão utilizados alguns conceitos sobre triangulação de Delaunay e diagrama de Voronoi, que podem ser encontrados em [2].
|
|
|
Figura 1 – Curva
recontruída
2.1 - Algoritmo Crust
O Crust é definido em [1] da seguinte forma:
Definição: Seja S um conjunto finito de pontos no plano, e V os vértices do diagrama de Voronoi do S ( vor(S) ). Seja S’ a união S U V, e considere a triangulação de Delaunay de S’ ( del(S’) ). Uma aresta da triangulação de Delaunay de S’ pertence ao Crust de S se ambos os vértices pertencem a S, ou alternativamente, se há um disco vazio em seu interior de pontos de S’ que toca os vértices da aresta.
Como uma aresta entre pontos de S pertencente a del(S’) também pertence a del(S), então o Crust é um subconjunto de del(S).
Com isso, pode-se obter o Crust utilizando o seguinte algoritmo, dado um conjunto S de amostras:
CRUST( S )
1. V <- conjunto de vértices do diagrama de Voronoi de S.
2. S' <- S U V
3. Obter a triangulação de Delaunay de S'.
4. Selecionar todas as arestas de del( S' ) que ligam pontos do conjunto S original.
Análise da complexidade do algoritmo para o pior caso:
1.A obtenção do diagrama de Voronoi de S pode ser realizada em O(n*logn) e a extração dos vértices leva O(n), pois o número de vértices é linear, o que dá O(n*logn) para este passo.
2.O(n).
3.A triangulação de Delaunay pode ser obtida em O(n*logn).
4.Como o número de arestas de del( S' ) é linear, este passo pode ser realizado em O(n), com uma estrutra de dados adequada.
Logo, o algoritmo tem complexidade O(n*logn).
2.2 – Algoritmo Beta-Skeleton
O Beta-Skeleton, introduzido por Kirkpatrick e Radke [3], é definido em [1], baseando-se na definição de uma região proibida, considerando uma constante beta >= 1:
Definição: Seja S um conjunto finito de pontos no plano, com pontos s1 e s2 pertencentes a S, a uma distância d(s1, s2) entre si. A região proibida de s1,s2 é a união dos dois discos de raio beta*d(s1, s2) / 2 tocando s1 e s2.
Definição: Seja S um conjunto finito de pontos no plano, com pontos s1 e s2 pertencentes a S. A aresta s1,s2 pertence ao Beta-Skeleton de S se a região proibida de s1,s2 estiver vazia.
Pela definição acima, se uma aresta pertence ao Beta-Skeleton, então há pelo menos um disco que contém apenas os pontos s1 e s2 na fronteira e nenhum outro no interior ou na fronteira. Logo o Beta-Skeleton de S, assim como o Crust, também é um subconjunto de del(S).
Assim podemos obter o Beta-Skeleton de um conjunto S de amostras e uma constante beta com o algoritmo abaixo:
BETA_SKELETON( S, beta )
1.Obter a triangulação de Delaunay de S.
2.Selecionar todas as arestas e, pertencentes a del( S ), para as quais os centros dos circuncírculos dos triângulos adjacentes a e estão em lados opostos em relação a e, e seu raio é maior que (beta/2)*(comprimento(e)).
Análise de complexidade para o pior caso.
1.A triangulação de Delaunay pode ser obtida em O(n*logn).
2.Como o número de arestas em del(S) é linear e o número de triangulos adjacentes é sempre constante (menor ou igual a 2), este passo pode ser realizado em O(n).
Logo, o algoritmo tem complexidade O(n*logn).
2.3 -
Condições de amostragem
Dadas as definições dos dois grafos acima, é necessário determinar as condições de amostragem em que essas abordagens garantem uma boa reconstrução da curva desejada.
Para isso, [1] introduz a função “Local Feature Size”, que permite que seja obtida uma medida da qualidade esperada para a reconstrução de uma curva:
Definição: Seja F uma curva suave, e um
ponto p pertencente a F. Então LFS(p) é a distância Euclidiana de p ao ponto m
mais próximo no eixo medial de F.
LFS(p) = d(p, m)
O eixo medial (figura 2) de uma curva F pode ser visto como o conjunto de pontos que são centros de discos vazios no interior que são tangentes a dois ou mais pontos de F. A união dos vértices do diagrama de Voronoi de um conjunto S de amostras de F dá uma aproximação do eixo medial da curva.
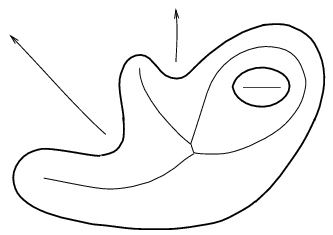
Figura 2
Com isso, pode-se definir a condição de amostragem de F (figura 3):
Definição: Uma curva suave F é r-amostrada
por um conjunto finito de pontos S se a distância de
todos os pontos p pertencentes a F a uma amostra s pertencente a S for menor ou
igual a r*LFS(p), ou seja, se:
d(p, s) =< r * d(p, m).
Podemos colocar r como uma razão:
r
= d(p, s) / d(p, m)
e testar se todo r da curva pertence ao intervalo desejado.
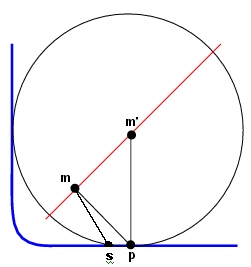
Figura 3
Se r < 1, pode ser demonstrado que del(S) contém uma aresta entre cada par de vértices adjacentes em F, ou seja, que a aproximação poligonal de F pelas amostras de S está contida em del(S). Além disso, é garantido um ângulo mínimo de (PI - 4*arcsin(r/2)) entre três amostras adjacentes em F, o que gera curvas suaves, de acordo com o valor de r.
2.4 - Critérios para
amostragem
Utilizando a medida de qualidade descrita acima, podemos procurar determinar critérios para a amostragem baseados em valores de r, onde uma curva é satisfatoriamente reconstruída.
É observado em [1] que, para uma curva r-amostrada, se r >= 1, então pode não haver reconstrução única para a curva. Assim, devemos explorar valores de r < 1.
O seguinte teorema também acrescenta informações interessantes:
Teorema: Seja uma curve suave F r-amostrada no
plano, com r < 1. Então a triangulação de Delaunay do conjunto de amostras S
contém uma aresta entre todos os pares de amostras adjacentes, ou seja, a
aproximação poligonal da curva está contida em del(S).
Logo, podemos criar algoritmos que extraem as arestas relativas a F, a partir da triangulação de Delaunay de S, para uma amostragem suficientemente densa.
Para o Crust e Beta-Skeleton, os critérios de amostragem são definidos pelos teoremas a seguir:
2.4.1
- Crust
Teorema: O
Crust de uma curva suave r-amostrada, com r < 0.4, contém uma aresta entre cada par de amostras
adjacentes em F.
Teorema: O Crust de uma curva r-amostrada não
contém nenhuma aresta entre vértices não adjacentes, para r < 0.252.
Para uma amostragem com r < 0.252, o Crust reconstrói univocamente a curva F.
2.4.2
- Beta-Skeleton
Teorema: Seja F uma curva suave r-amostrada por um
conjunto S de pontos, e r <= 0.297.
O Beta-Skeleton de S contém exatamente as arestas entre vértices adjacentes,
para beta = 1.70.
O valor de beta apresentado acima é o que permite a amostragem mais esparsa possível, segundo [1].
2.5 - Comentários
adicionais
Para Crust, é importante achar os vértices do diagrama de Voronoi V porque eles nos permitem achar uma aproximação do eixo medial da curva que se encontra definida pela amostragem S. O eixo medial “separa” dois lados de uma curva fechada ou com concavidades, evitando que, ao realizar a triangulação de Delaunay de S U V, haja arestas conectando esses dois lados. Assim, removemos automaticamente arestas que não são boas candidatas à reconstrução.
Para os testes que realizamos, o Crust apresentou melhores resultados que o Beta-Skeleton, no caso geral, recontruindo as curvas mais próximas às que esperávamos.
Uma vantagem do Beta-Skeleton é que a variação do parâmetro beta nos permite acondicionarmos nosso algoritmo a certas condições de densidade de amostragem, podendo, em alguns casos, melhorar um pouco o resultado em relação ao Crust.
Os dois algoritmos dependem dos critérios de amostragem definidos anteriormente. Um problema desses critérios é que, no caso de curvas com cantos vivos (“sharp corners”), o parâmetro r tenderá a zero próximos a esses pontos e o critério obrigará uma amostragem infinita nesses locais. O algoritmo Gathan, apresentado a seguir, se propõe a tratar de curvas com cantos vivos, utilizando outros critérios.
3. Tratamento de curvas com sharp corners (cantos vivos)
3.1 - Gathan
Os algoritmos anteriores definem a densidade de amostragem necessária através de um parâmetro ε, requisitando que cada ponto pertencente à curva possua uma amostra distando ao máximo ε f(p), onde f(p) é a distância de p ao eixo medial da curva.
Esta condição de densidade de amostragem funciona bem para curvas suaves. No entanto, em se tratando de curvas com sharp corners (cantos vivos) esta condição não pode ser satisfeita: é necessária uma amostragem infinita perto dos cantos. Logo, os algoritmos anteriores não funcionam para curvas desse tipo, como ilustra a figura abaixo.
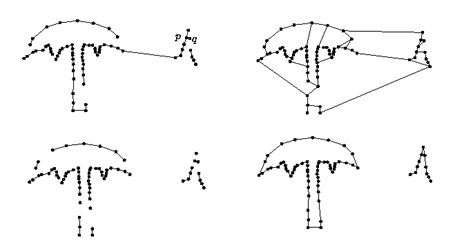
Figura 4 - Saída de Crust (acima-esquerda), NN-Crust
(acima-direita), Conservative-Crust (abaixo-esquerda), Gathan (acima-direita)
3.1.1
- Trabalhos Anteriores
O primeiro algoritmo capaz de lidar com curvas com cantos foi desenvolvido por Giesen. Ele provou que o problema do Caixeiro Viajante reconstrói uma curva com cantos se a densidade da amostragem é superior a um certo valor de referência. Este valor depende dos ângulos entre as tangentes esquerda e direita nos cantos da curva.
Mas esta solução tem duas grandes desvantagens. Primeiro, ela não oferece uma boa reconstrução para curvas de vários componentes, visto que ela irá conectá-los com um caminho para resolver o problema. Segundo, não é claro se este algoritmo pode ser generalizado para três dimensões.
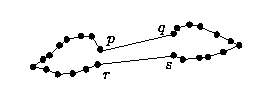
Figura 5 - O algoritmo de Caixeiro Viajante conecta dois
componentes da curva com arestas inválidas pq e rs.
Este novo algoritmo não possui uma prova teórica de sua corretude. Porém, resultados práticos indicam que sua reconstrução é superior a deste algoritmo baseado no Caixeiro Viajante, bem como a dos algoritmos de Crust e B-Skeleton.
3.1.2
- Cantos
A curva deve ser planar e simples (sem auto interseção), embora possa ter vários componentes. Além disso, tangentes à esquerda e à direita são definidas em qualquer ponto e são iguais em todos os pontos, exceto em pontos isolados denominados cantos, onde fazem um ângulo menor que π. A curva pode ser fechada ou ter pontos de término. Cantos são pontos isolados e não precisam estar no conjunto de amostras. A única exigência é que a vizinhança de um canto deve ser amostrada de forma densa.
As amostras dividem a curva em arcos. Cada amostra é adjacente a dois arcos. Uma amostra é regular se os arcos adjacentes não contém uma amostra corner ou boundary. Uma amostra é corner se é um canto da curva ou se pelo menos um arco adjacente contém uma amostra corner. Uma amostra é boundary se é um ponto de término ou se pelo menos um arco adjacente contém uma amostra boundary. Assume-se que a amostragem é densa o suficiente de forma a não existir uma amostra que seja adjacente a uma amostra corner e a uma amostra boundary. Uma aresta é correta se conecta duas amostras adjacentes na curva.
O algoritmo se baseia nas estimativas das normais das amostras. Elas podem ser estimadas utilizando uma técnica de poles [4]. É relativamente fácil estimar as normais em amostras regulares. Já as amostras corner ou boundary são mais complicadas e em consequência oferecem dificuldade para o processo de reconstrução. Entretanto, as amostras regulares vizinhas podem ser usadas para determinar arestas que devem ser incidentes às amostras corner e boundary. No caso de arestas que devem unir duas amostras corner? Existem dois casos distintos, ilustrados na figura abaixo. As amostras corner p1 e p2 à esquerda se comportam de forma diferente das amostras corner p3 e p4 à direita. A amostra p3 se comporta como um verdadeiro canto da curva. O algoritmo então consegue estimar a normal em p4 embora seja uma amostra corner. Estimar a normal tanto em p1 como em p2 é mais difícil. Logo, detectar p1p2 é mais difícil do que detectar p3p4. A estimativa incorreta das normais leva ao aparecimento de arestas inválidas. Mas estas arestas podem ser removidas ao final do algoritmo.
3.1.3
- O Algoritmo
Os algoritmos anteriores assumem que a amostragem da curva é suficientemente densa através da seguinte condição:
Condição (R): Qualquer ponto na curva amostrada possui
uma amostra a uma distância de no máximo ε < 1 vezes a sua distância ao
eixo medial.
Como foi visto anteriormente, esta condição não pode ser satisfeita na prática para curvas não suaves. Logo, uma nova condição de amostragem é necessária próximo aos cantos.
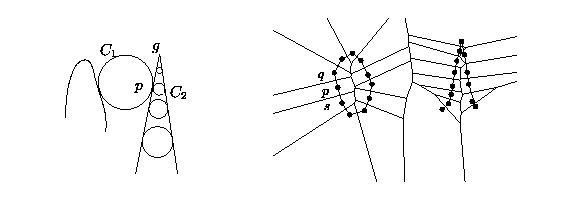
Figura 6
Assumindo g um ponto de canto da curva. Em cada ponto p da curva há dois círculos maximais C1 e C2 que tocam a curva tangencialmente em p e pelo menos em algum outro ponto, ou são infinitos. À medida em que p se aproxima de g, o raio de um desses círculos se aproxima de zero. A condição (R), de certa forma, depende do menor dos dois círculos e então requer densidade infinita perto de g. Se modificarmos a condição de amostragem em uma pequena vizinhança dos cantos de forma que ela dependa do maior dos dois círculos, este problema não acontece. Ao mesmo tempo, o ângulo өg entre a tangente esquerda e o reverso da tangente direita de g deve também influenciar a condição de amostragem perto de g. Quanto menor o ângulo, mais densa deve ser a amostragem. Estes conceitos estão melhor formalizados na condição abaixo.
Considere uma bola com centro em g , crescendo enquanto sua borda intercepta o eixo medial em apenas um ponto. Assuma rg o raio desta bola. Assuma uma bola protetora com centro em g e raio crg para alguma constante c < 1, por exemplo c = 1/6.
Condição (R’): p qualquer
ponto da curva. Se p está na bola
protetora de um canto g, deve ter uma
amostra a uma distância máxima de krgөg,
caso contrário p deve ter uma amostra
a uma distância máxima de εf(p),
onde k < c < 1 e ε < 1 são constantes viáveis.
Apesar o algoritmo não utilizar a condição R’ explicitamente para escolher as arestas, a lógica utilizada pode ser explicada por ela.
A relação entre a lógica do algoritmo e a condição R’ é explicada no artigo original [4].
3.1.4
- Estimando as normais
Amenta e Bern [4] mostram que, dado que a condição R de amostragem é satisfeita, as normais das amostras de uma superfície podem ser estimadas através de suas células de Voronoi. Eles introduziram o conceito de poles: são os vértices mais distantes das amostras nas suas respectivas células de Voronoi. Se a célula de voronoi é limitada, a normal pode ser estimada como sendo a linha que passa pela amostra e seu pole. Caso a célula seja ilimitada, a normal pode ser estimada como sendo a média dos raios ilimitados da célula.
Este procedimento também pode ser utilizado para o caso de curvas. O argumento pode ser encontrado no artigo original [5].
3.1.5
- Vizinhos mais próximos
Uma vez estimadas as normais, a estratégia de vizinhos mais próximos pode ser utilizada: cada amostra p se conecta ao vizinho mais próximo de cada lado de sua normal. Entretanto, deve-se ter cuidado para não escolher arestas cujas normais formem ângulos grandes com a normal estimada da amostra.
3.1.6
- Vizinhos mais próximos – limitando o ângulo
A figura abaixo mostra um exemplo onde a estratégia de vizinhos mais próximos escolhe uma aresta inválida pq, com sua normal fazendo um ângulo próximo de 90 graus com a normal estimada de p. Para evitar esse problema, é introduzida a condição de ângulo.
Condição de ângulo: Uma aresta pq se candidata ao
teste de vizinho mais próximo somente se sua aresta dual de Voronoi faz um
ângulo agudo menor que um parâmetro α definido pelo usuário com a normal
estimada de p.
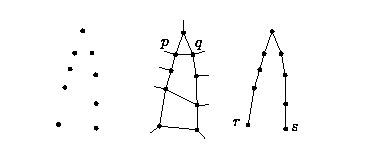
Figura 7
Resultados mostraram que um valor entre 35 e 40 graus é uma boa escolha para α na maioria dos casos. É importante salientar que esta restrição também permite a detecção de pontos de término na curva.
3.1.7
- Vizinhos mais próximos – condição de rateio
A condição de ângulo sozinha não é suficiente para descartar arestas inválidas. A figura abaixo ilustra esse problema. Os pontos p e r não devem ser unidos por uma aresta. Entretanto a aresta dual de Voronoi de pr passa pela condição de ângulo, da mesma forma que a aresta correta pq. A técnica de vizinho mais próximo irá selecionar a aresta pr por estar mais próxima do que pq. Isso acontece pois a curva possui é pouco amostra, segundo a condição R, perto do canto.
Observa-se que a relação entre o comprimento da aresta dual de voronoi de pq e seu comprimento é muito maior que a mesma relação aplicada a pr. A condição de amostragem R’ certifica que arestas corretas sempre possuirão uma relação maior do que as possíveis arestas incorretas. Daí surge uma nova condição, a condição de rateio.
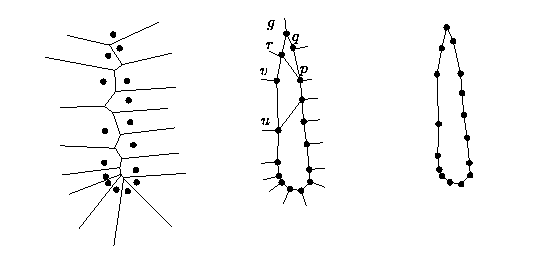
Figura 8
Condição de rateio: A relação entre o comprimento da aresta dual de Voronoi e o comprimento da aresta correspondente deve ser maior que um parâmetro ρ.
Resultados mostraram que a faixa 1.7 – 2.0 funciona melhor para ρ na maioria dos casos.
3.1.8
- Vizinhos mais próximos – Condição topológica
Ao final deste processo, algumas arestas inválidas podem ser escolhidas, apesar da técnica escolher no máximo duas arestas incidentes para cada amostra. Isso de deve ao fato da estimativa das normais nos cantos ser incorreta. Esse problema pode ser resolvido da seguinte forma: basta, para cada amostra, deixar apenas as duas arestas incidentes de menor tamanho, removendo as outras, caso existam.
O argumento que justifica este processo pode ser encontrado no artigo original [5].
3.1.9
- Pseudocódigo do algoritmo
GATHAN( P, α, ρ)
1. Computar o diagrama de Voronoi Vp
2. Para cada ponto p pertencente a P faça
a. Computar o pole e a normal de p
b. Assuma E o conjunto de arestas de Delaunay incidentes a p satisfazendo:
i. normal de cada e pertencente a E faz ângulo agudo menor que α com a normal
ii. h/l > ρ onde l e h são os comprimentos de e e sua aresta dual de Voronoi
c. Mantenha apenas as menores arestas pq e ps pertencentes a E de cada lado da normal
3. Remova qualquer aresta que não esteja entre as duas menores arestas que incidem sobre uma amostra.
3.1.10
- Conclusão
O algoritmo pode ser “calibrado” com os parâmetros α e ρ, porém para valores entre 35 e 40 graus e um valor de 1.7, respectivamente, mostrou um bom resultado na maioria dos casos. Sem dúvida em se tratando de curvas não suaves, este algoritmo produz uma boa reconstrução, mesmo não possuindo uma prova teórica de sua corretude.
Exemplos de valores para α e ρ em diversos casos podem ser encontrados no artigo original [5].
4. Referências
[1] Amenta N.,
[2] P. C. P. Carvalho e L. H. de Figueiredo, “Introdução à Geometria Computational”, 18° Colóquio Brasileiro de Matemática, IMPA, 1991.
[3] Kirkpatrick, D. G. and Radke, J.D., “A framework
for computational morphology”, Computational
Geometry (G. Toussaint, ed.), North-Holland (1998), pp. 217-248.
[4] Amenta, N. and
[5] Dey, T. K. and Wenger, R., “Reconstructing Curves
with Sharp Corners”, June 2000.